重点与难点

  • 关系元组演算公式的递归定义，关系域演算公式的递归定义
  • 关系元组演算公式：与 、或 、非 、存在量词 、全称量词 
  • 用关系元组运算公式表达查询的思维训练
  • 用QBE语言表达查询的思维训练
  • 关系元组演算、域演算与关系代数在表达查询方面的思维差异

一. 关系演算之关系元组运算

1. 概述

  • 关系演算 以数理逻辑中的谓词演算为基础，是描述关系运算的另一种思维方式
  • 按谓词变量的不同，分为关系元组演算和关系域演算
    • 关系元组演算 是以元组变量 作为谓词变量的基本对象
    • 关系域演算 是以域变量 作为谓词变量的基本对象

2. 关系元组演算的形式

关系元组演算公式的基本形式：，表示所有使谓词 为真的元组 的集合。

  • 是元组变量； 表示元组 在关系 中； 表示元组 的分量，即 在属性 上的值； 是与谓词逻辑相似的公式， 表示以元组 为变量的公式， 表示以元组 为变量的公式

公式 的递归构造：

  • 三种原子公式：
  • 是公式， 也是公式
  • 也是公式
  • 如果 是公式， 是关系，则 也是公式
  • 上述运算符优先级降序：括弧、、、、、、
  • 元组演算公式只限于以上形式

3. 原子公式和与或非的理解运用

4. 存在量词与全称量词的理解与运用

被 、 限定的元组变量 ，称为“约束变量”，否则称为“自由变量”

例1：检索出年龄不是最小的所有同学

关系元组演算：

关系代数：

例2：检索出课程都及格的所有同学 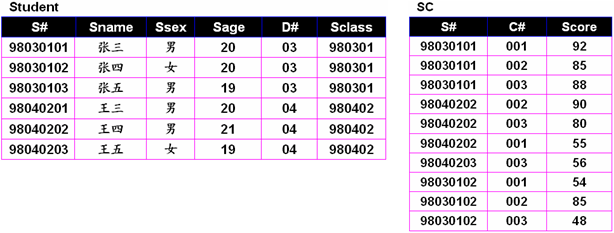image-20220304201113073

例3：检索计算机系的所有同学 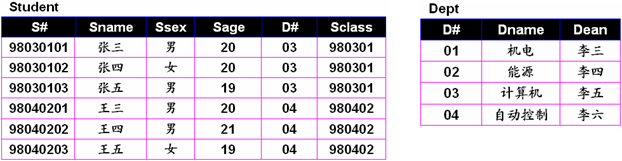计算机 image-20220304201035253

例4：检索年龄比张三小的所有同学 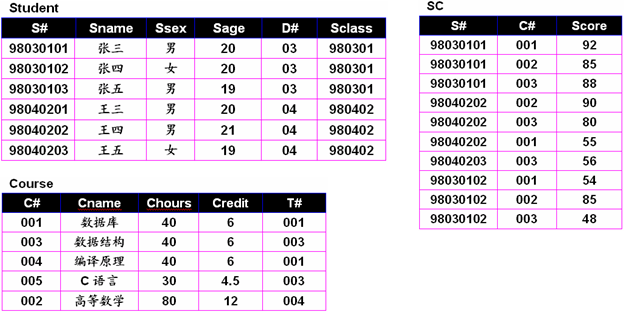张三 例5：检索学过所有课程的同学 image-20220304201509293

5. 应用训练语义正确性与等价性变换

6. 四个最复杂的例子

学生关系：

课程关系：

选课关系：

  • 全都学过 ：求学过李明老师教授所有课程的学生姓名

$$ {Sname,Cid}(Student SC Course) {Cid}(_{Tname="李明"}(Course)) \

{ t[Sname] | t Student (uCourse u[Tname]="李明")((wSC)(w[Sid]=t[Sid] w[Cid]=u[Cid])) } $$

  • 全没学过 ：没学过李明老师任一门课程的学生姓名（全部学生减去学过至少一门的）

李明李明

  • 至少有一学过 ：至少学过一门李明老师讲授课程的学生姓名

$$ {Sname}({Tname="李明"}(Student SC Course)) \

{ t[Sname] | t Student  (w SC w[Sid]=t[Sid])((uCourse u[Tname]="李明")(w[Cid]=u[Cid])) } \

{ t[Sname] | t Student  (w SC )(uCourse )(w[Sid]=t[Sid] w[Cid]=u[Cid] u[Tname]="李明") } $$

  • 至少有一没学过 ：至少有一门李明老师讲授课程没有学过的学生姓名

$$ {Sname}(Student)- {Sname,Cid}(Student SC Course) {Cid}({Tname="李明"}(Course)) \

{ t[Sname] | t Student  (uCourse u[Tname]="李明")((wSC)(w[Sid]=t[Sid]w[Cid]=u[Cid])) } $$

7. 关系代数转换为元组演算

并：

差：

交：

广义笛卡尔积：

选择：

投影：

元组演算公式总结：

  • 用递归定义公式，组合、递归地构造公式
  • 一种用逻辑表达查询的思维
  • 以元组为基本单位进行循环，先找到元组，再找到元组分量，进行谓词判断
  • 元组演算与关系代数可以相互转换（有前提，后面介绍）

二. 关系演算之关系域演算

1. 关系域演算公式

关系域演算公式的基本形式：，其中 代表域变量或者常量， 是以 为变量的公式，可以递归地构造：

  • 三种形式的原子公式

域变量 与常量 之间的比较关系：

域变量 与域变量 之间的比较关系：

  • 是公式， 也是公式
  • 也是公式
  • 如果 是公式， 是域变量，则 也是公式
  • 上述运算符优先级降序：括弧、、、、、、
  • 元组演算公式只限于以上形式

2. 关系域演算公式的构造

例1： 检索出不是03系的所有学生 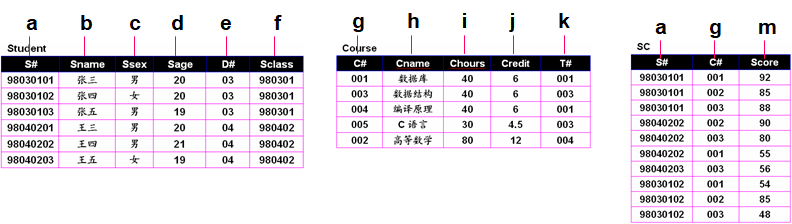例2： 检索不是（小于20岁的男同学）的所有同学的姓名 男 例3： 检索成绩不及格的同学姓名、课程及其成绩 image-20220306124631002

3. 关系域演算与关系元组演算的比较

  • 元组演算是以元组为基本处理单位和变量
  • 域演算是以域变量为基本处理单位（过程性差，非过程性的语言，适合最终用户）
  • 公式的运算符是相同的，只是变量不同
  • 元组演算和域演算可以等价互换

4. 关系域演算语言 QBE

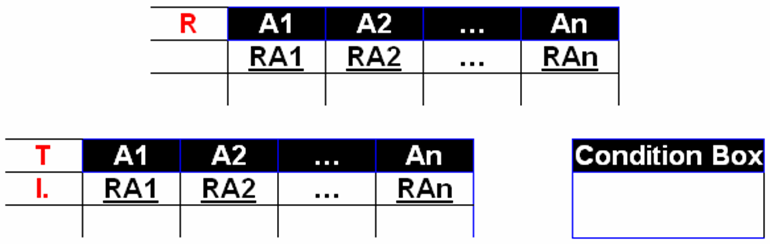
QBE（Query By Example）：高度非过程化的语言，适合终端用户的的使用，只需将条件填写在表格中

  • 关系名区：用于书写欲待查询的关系名
  • 属性名区：用于显示对应关系名区关系的所有属性名
  • 操作命令区：用于书写查询操作命令
    • Print或P.——显示输出操作
    • Delete或D.——删除操作
    • Insert或I.——插入操作
    • Update或U.——更新操作
  • 查询条件区：用于书写查询条件

image-20220306161741998

例：查询条件——不同属性上的与条件：找出年龄小于17岁的所有女同学

image-20220306161936516

例：查询条件——示例元素与投影：找出年龄小于17岁的所有女同学的姓名

image-20220306162044557

条件 参量中的参量也可以是域变量，用任何一个值（不必是结果中的值带）有下划线表示，被称为示例元素. 示例元素下划线上面的值不起作用，被当作域变量名称来对待，只用于占位或是连接条件。

例：查询条件——用示例元素实现与和或：多行书写，用不同（或相同）的示例元素来表征或运算（与运算）

image-20220306162621497

image-20220306162629782

例：查询条件——相当于括号的条件表示：将 、、 条件写在操作命令区（对整行条件而言）

image-20220306162901133

例：查询条件——用示例元素实现多个表的连接：李明老师教过的所有学生（当检索涉及多个表时，可利用同一连接条件使用相同的示例元素，来实现多个表的连接.）

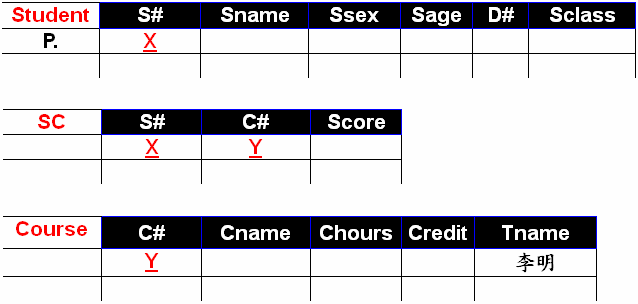
image-20220306162951708

5. QBE 语言应用训练

例：查询计算机系年龄大于19岁的男同学的姓名（张三不表示值）

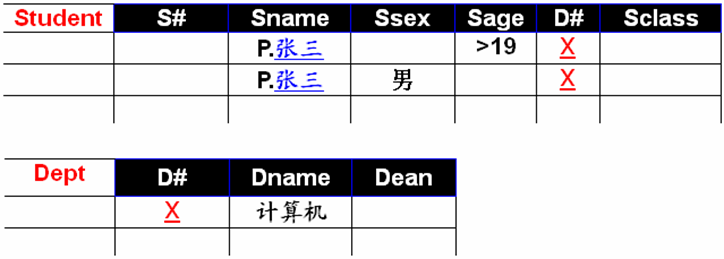
image-20220306163343122

例：查询计算机系或者年龄大于19岁或者是男同学的姓名

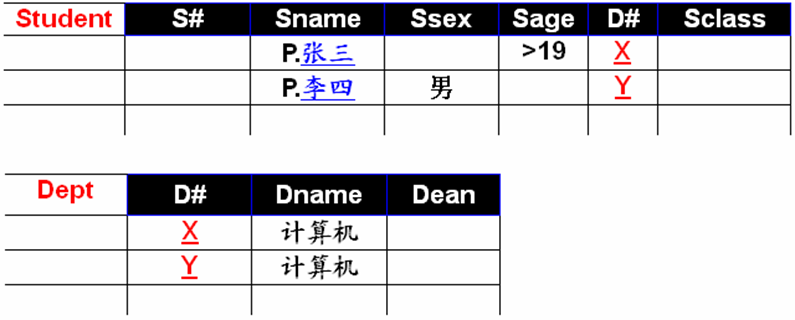
image-20220306163533664

例：找出比男同学张三年龄大的所有男同学的姓名

image-20220306163712563

例：将张三同学的年龄更新为19岁

image-20220306164226192

例：将每位同学的年龄增加1岁

image-20220306164233237

例：找出成绩不及格同学的姓名及不及格的课程和分数

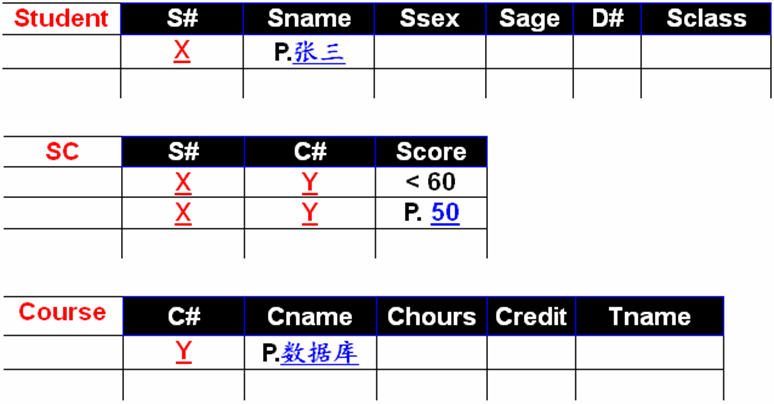
image-20220306164300402

例：

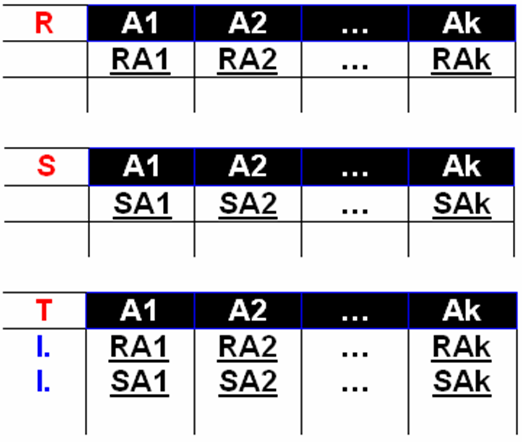
image-20220306164340275

例：

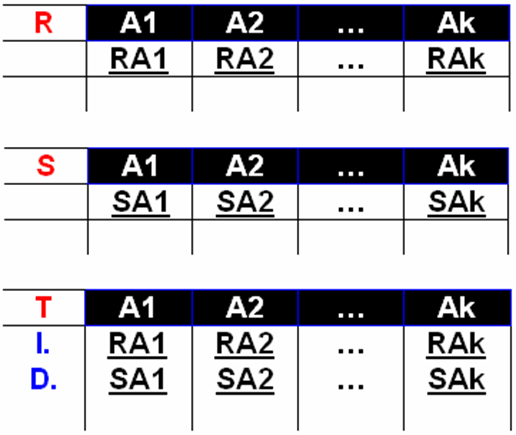
image-20220306164406638

例：

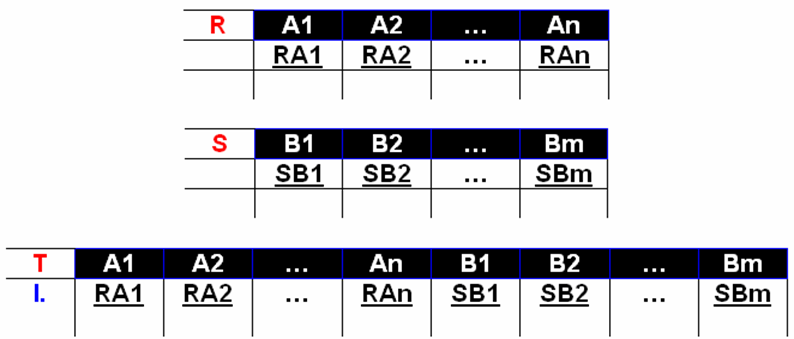
image-20220306164448182

例： ，其中 是某一个

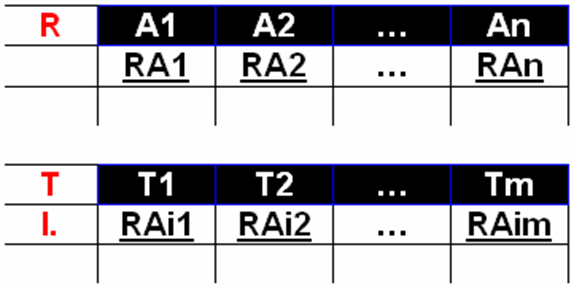
image-20220306164557078

例：

image-20220306164756907

三. 关系演算之安全性

关系运算的安全性：不产生无限关系和无穷验证的运算

  • 关系代数是集合运算，是安全的（集合有限，运算次数有限）
  • 关系演算不一定安全
    • 无限关系：
    • 无穷验证： 验证所有元素为真或假

安全约束有限集合 DOM

  • 是一个有限集合，其中的每个符号要么是 中明显出现的符号，要么是出现在 中的某个关系的 某元组的分量。
  • 主要用于约束 中一些谓词的计算范围，它不必是最小集合。

安全元组演算表达式，满足以下三个条件：

  • 只要 满足 ， 的每个分量就是 的一个成员
  • 对于 中形如 的子表达式，若 满足 ，则 的每个分量都是 中的成员（ 外的元素无需验证，默认不满足）
  • 对于 中形如 的子表达式，若 不满足 ，则 的每个分量都是 中的成员（ 外的元素无需验证，默认满足）

四. 三种关系运算的观点

  • 关系代数——以集合为对象的操作思维，由集合到集合的变换

  • 元组演算——以元组为对象的操作思维，取出关系的每一个元组进行验证，有一个元组变量则可能需要一个循环，多个元组变量则需要多个循环

  • 域演算——以域变量为对象的操作思维，取出域的每一个变量进行验

  • 三种运算之间是等价的

    • 关系代数与安全的元组演算表达式与安全的域演算表达式是等价的。即一种形式的表达式可以被等价地转换为另一种形式

  • 三种关系运算都可说是非过程性的

    • 相比之下：域演算的非过程性最好，元组演算次之，关系代数最差

  • 三种关系运算虽是抽象的，但却是衡量数据库语言完备性的 基础